CBSE Notes for Class 6 Maths Chapter 1 Knowing our Numbers Summary is highly helpful for students who want to understand all the exercise questions. NCERT Class 6 Maths Notes and Practice Problems have been reviewed by our best Mathematics teachers. We have provided detailed notes and all the solutions for NCERT Maths class 6 Knowing our Numbers. so that you can solve the questions in class 6 mathematics textbook seamlessly. CBSE worksheets for class 6 Maths are available at free of cost to all the students.
Board: Central of Secondary Education
Class: Class 6
Subject: Maths
Chapter Name: Knowing Our Numbers
Comparing Numbers :
As we have done quite a lot of this earlier, let us see if we

How many numbers can we make?
Suppose, we have four digits 1, 2, 3, 4. Using these digits we want to make different 4-digit numbers such that no digits are repeated in a number. Thus, 3241 is allowed but 1123 is not. The greatest number is 4321 and the smallest is 1234.
Ex: Use the given digits without repetition and make the greatest and smallest 4-digit numbers.
(a) 2, 8, 6, 1
(b) 3, 0, 7, 4
(c) 8, 9, 2, 3
(d) 5, 0, 8, 2
Sol:
(a) Greatest number is 8621, Smallest number is 1268
(b) Greatest number is 7430, Smallest number is 3047
(c) Greatest number is 9832, Smallest number is 2389
(d) Greatest number is 8520, Smallest number is 2058
Ascending order:
Ascending order means arrangement from the smallest to the greatest.
Ex. 847, 9754, 8320, 571
Sol. 571, 847, 8320, 9754
Descending order:
Descending order means arrangement from the greatest to the smallest.
Ex. 847, 9754, 8320, 571
Sol. 9754, 8320, 847, 571
Introducing 10,000:
We observe that :
Greatest single digit number+1 = smallest 2-digit number
9 + 1 = 10
Greatest 2-digit number + 1 = smallest 3-digit number
99 + 1 = 100
Greatest 3-digit number + 1 = smallest 4-digit number
999 + 1 = 1000
Greatest 4-digit number + 1 = smallest 5-digit number
9999 + 1 = 10,000
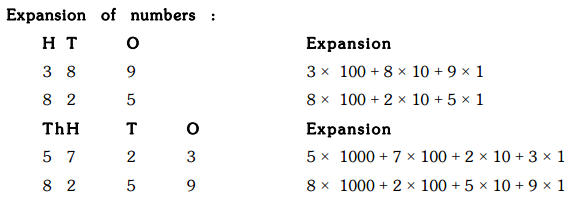
Remember :
1 hundred = 10 tens
1 thousand = 10 hundreds = 100 tens
1 lakh = 100 thousands = 1000 hundreds
1 crore = 100 lakhs = 10,000 thousands
Use of Commas:
1. Indian System of Numeration: In our Indian System of Numeration we use one, tens, hundreds, thousands and then lakhs and crores. The first comma comes after hundreds place (three digits from the right) and marks thousands. The second comma comes two digits later (five digits from the right). It comes after ten thousands place and marks lakh. The third comma comes after another two digits (seven digits from the right). It comes after ten lakh place and marks crore.
For example, 5, 78, 21, 623
2. International System of Numeration: In the International System of Numeration, as it is being used we have ones, tens, hundreds, thousands and then millions. One million is a thousand thousands. Commas are used to mark thousands and million. It comes after every three digits from the right. The first comma mark thousands and the
next comma marks millions.
For example, 57, 821, 623
Remember:
10 millimetres = 1 centimetre
1 metre = 100 centimetres = 1000 millimetres
1 kilometre = 1000 metres = 10,00,000 millimetres
1 gram = 1000 milligram
1 litre = 1000 millilitres.
Solved Examples:
Ex 1.
Insert commas suitably and write the names according to Indian System of Numeration :
(a) 87595762
(b) 8546283
(c) 99900046
(d) 98432701
Sol:
(a) 8,75,95,762 = Eight crore seventy-five lakh ninety-five thousand seven hundred sixty two.
(b) 85,46,283 = Eighty-five lakh forty-six thousand two hundred eighty-three.
(c) 9,99,00,046 = Nine croe ninety-nine lakh forty six.
(d) 9,84,32,701 = Nine crore eighty-four lakh, thirty-two thousand seven hundred one.
Ex 2.
Insert commas suitably and write the names according to International System of Numeration :
(a) 78921092
(b) 7452283
(c) 99985102
(d) 48049831
Sol.
(a) 78,921,092 = Seventy-eight million, nine hundred twenty-one thousand, ninety-two.
(b) 7,452,283 = Seven million four hundred fifty-two thousand two hundred eighty-three.
(c) 99,985,102 = Ninety-nine million nine hundred eighty-five thousand, one hundred two.
(d) 48,049,831 = Forty-eight million forty-nine thousand eight hundred thirty one.
Ex 3.
Population of Kota was 5,48,985 in the year 1995. In the year 1996 it was found to be increased by 1221. What was the population of the city in 1996?
Sol.
Population of the city in 1996
= Population of the city in 1995 + Increase in population
= 5,48,985 + 1221
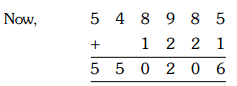
Types of Numbers:
(i) Natural Numbers: (N)
Set of all counting numbers from 1 to+∞,N = {1,2,3,4,… ∞}.
(ii) Whole Numbers: (W)
Set of all natural numbers including zero, W = {0,1,2,3,4,… }
(iii) Integers:
Set of all positive and negative of natural numbers including zero from – ∞, to + ∞, I or Z = {…,-3, -2, -1, 0, 1, 2, 3,
…}.
Positive integers {1, 2, 3, 4 }
Negative integers { -3, -2, -1}
(iv) Rational Numbers:
These are real numbers which can be expressed in the form of p/q, where p and q are integers and q ≠ 0. e.g., 2/3, 37/15, /17/19 etc.
All the integers are rational numbers, because every integer can be expressed in the form p/q. For example, the integers
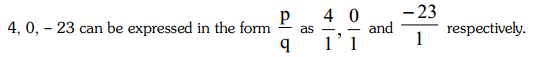
Note:
1. All the fractions are rational numbers.
2. Every natural number is a rational number.
3. Every whole number is a rational number.
4. Every integer is a rational number.
5. Every fraction is a rational number.
Density property of rational numbers:
Between any two different rational numbers, there are infinitely many rational numbers. To find many rational numbers between two given distinct rational numbers, use the following method.
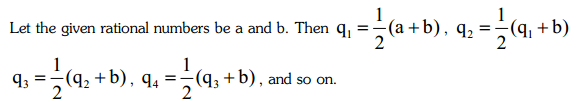
Here q1, q2, q3, q4……….. are the rational numbers between two distinct rational numbers a and b.
Ex 1.
Find three rational numbers between 1/5 and 1/3.
Sol.
Let q1, q2, q3 be the three required rational numbers. Then

Comparison of two rational numbers:
Using the arithmetical process:
- Express each rational number with a positive denominator
- Find LCM of the positive denominators
- Express each of the given rational numbers with LCM as the common denominator
- The number having greater numerator is greater
To compare two rational numbers p/q and r/s. we compare the products s × p and q × r and define their inequality as under
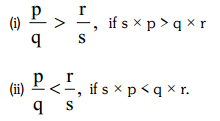
Properties of rational number:
Decimal representation of a rational number:
We can represent a rational number as a decimal number by the long division process. We have three types of decimals. They are
- Terminating decimals
- Non-terminating and repeating decimals
- Non-terminating and non-repeating decimals
- Defination of terminating, non-terminating, recurring & non-recurring.
Ex.2:
√2, √3 etc.
Converting a decimal number into an equivalent rational number in the form of a/b
We can divide this into two parts :
Case – 1: When the decimal number is a terminating number. Express 0.3 as a rational number.
Sol.
0.3 = 3/10

Introduction of irrational numbers:
Every rational number can be expressed either in terminating decimal form or non-terminating repeating (or periodic) decimal form. Consider the decimal number 0.1010010010001 We can see that no group of digits is repeating in a cyclic manner. So we have numbers whose decimal representation is neither terminating nor repeating. There are a number of such decimals. Such numbers are called irrational numbers.
Note:
A number is an irrational number, if it has a non-terminating and non-cyclic repeating decimal representation.
Real Numbers:
The set of rational numbers together with the set of irrational numbers are called ‘Real Numbers’, denoted by “R”
Whole Numbers:
The natural numbers along with zero form the collection of whole numbers. 0, 1, 2, 3, 4, 5, are whole numbers.
Successor:
Success of every number comes just after the number. Therefore, the successor of every number is obtained by adding 1 to the number.
For example: successor of 98 = 98 + 1 = 99
Predecessor:
Predecessor of every number comes just before the number.
For example: predecessor of 98 = 98 – 1 = 97
Representation of Numbers on Number Line:
Every number on number line represents position from its greater and smaller numbers. Negative, positive, whole, natural, prime, etc. All are represented on number line.
Numbers on number line are represented by the following:
Step 1:
Draw a line and mark a point zero on it.
Step 2:
Distance between the numbers is always equal. Therefore, the length of number line should be divided into required into required number of interval.
Step 3:
The arrow mark at the far end point of number line, indicates infinitive.
Ex:
Representation of whole numbers from 0 to 10 on number line.
Step 1:
Draw a horizontal line and mark a point 0 on it.
Step 2:
Mark another point and divide the distance among them into 10 equal parts.
Step 3:
Write numbers 1 to 10 at each division.

Properties of whole numbers:
1. Addition:
Sum of any two whole numbers is always a whole number i.e. the collection of whole numbers is closed under addition.
For example : 2 + 3 = 5
2. Substraction:
Substraction of any two whole number is not always a whole number.
For example : 3 – 2 = 1 (whole number). But 2 – 3 = -1 (not whole number)
3. Multiplication:
Multiplication of any two whole number is always a whole number.
For example : 2 × 3 = 6, 2 × 0 = 0.
4. Division:
Division of any two whole number is not always a whole number.
For example : 6/3 = 2 (is whole number) 2/3 = (not a whole number)
3/0 (not possible)
Solved Examples:
Problem 1.
Add the following:
347 + 578 + 153
Sol.
We can group the numbers in different ways.
As 347 + 153 = 500,
So, we can group
347 + 578 + 153 = (347 + 153) + 578 = 500 + 578 = 1078
Problem 2.
Show that:
(63 + 49) + 37 = 63 + (49 + 37)
Sol.
(63 + 49) + 37 = 112 + 37 = 149
63 + (49 + 37) = 63 + 86 = 149
(63 + 49) + 37 = 63 + (49 + 37)
Problem 3.
Solve by suitable rearrangement.
32 × 25
Sol.
32 is equal to 8 × 4
So, 32 × 25 = 8 × 4 × 25
= 8 × (4 × 25)
= 8 × 100 = 800
Problem 4.
Simplify using properties .
4 × 16 × 125
Sol.
4 × 125 = 500
So, 4 × 16 × 125 = 16 × 4 × 125 = 16 × (4 × 125)
= 16 × 500 = 8000
Problem 5.
A florist arranges 6 gladioli and 7 roses in a bouquet. Raj buys 5 such bouquets for the school annual function. What is the total number of flowers in these 5 bouquets?
Sol.
Gladioli in 5 bouquets = 5 × 6 flowers = 30 flowers Rose in 5 bouquets = 5 × 7 flowers = 35 flowers Total number of flowers in 5 bouquets = (5 × 6) + (5 × 7) = 65 flowers Another ways of solving the problem is as follows.
Flowers in one bouquets (gladioli = roses) = (6 + 7) flowers
Total number of flowers in 5 bouquets = 5 (6 + 7) flowers = 5 × 13 flowers = 65 flowers
So, 5(6 + 7) = (5 × 6) + (5 × 7)
5 × 13 = 30 + 35
65 = 65
Hence, we can conclude that if a, b and c are whole numbers,
then a × (b + c) = a × b + a × c
This property is called the distributive property of multiplication over addition.
Problem 6.
7 × (8 + 3) = 7 × 8 + 7 × 3
Sol.
We can see that multiplication is distributed between 8 and 3 when the sign is one of addition.
Let us look at another example.
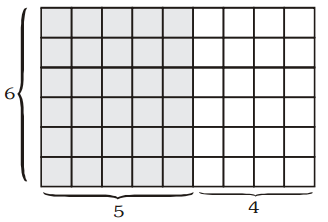
6 rows of 5 squres + 6 rows of 4 squares
= 5 x 6 + 4 × 6 = 30 + 24 = 54 squares.
This is also equal to 6 rows of 9 squares.
6 × 9 = 54
So, 5 × 6 + 4 × 6 = 6 (5 + 4)
30 + 24 = 6 × 9
54 = 54
Problem 7.
There are 7 plates. Six biscuits are placed on each plate. If 4 biscuits are taken away from each plate, how many biscuits are left on the plates ? Write the mathematical statement.
Sol.
Biscuits on 7 plates = 7 × 6 = 42 biscuits
Biscuits taken away from 7 plates = 7 × 4 = 28 biscuits
Biscuits remaining = 7 × 6 – 7 × 4
= 42 – 28 = 14 biscuits
or, Biscuits left on one plate = (6 – 4) biscuits
Biscuits left on 7 plates = 7(6 – 4) biscuits
= 7 × 2 biscuits = 14 biscuits
So, the mathematical statement
7 × (6 – 4) = 7 × 6 – 7 × 4
Problem 8.
Write the place values of the bold digits in each of the following :
(a) 370345
(b) 2479034
(c) 42371509
Sol.
(a) The place value of 7 in 370345 is 70,000.
(b) The place value of 2 in 2479034 is 20,00,000.
(c) The place value of 1 in 42371509 is 1,000.
Problem 9.
Write the following numbers in expanded notation.
(a) 4,89,342
(b) 31,85,204
(c) 3,24,05,620
Sol.
(a) 4,89,342 = 4,00,000 + 80,000 + 9,000 + 300 + 40 + 2
(b) 31,85,204 = 30,00,000 + 1,00,000 + 80,000 + 5,000 + 200 + 4
(c) 3,24,05,620 = 3,00,00,000 + 20,00,000 + 4,00,000 + 5,000 + 600 + 20
Problem 10.
Write the following numbers in standard numerals.
(a) 1,00,000 + 70,000 + 8,000 + 900 + 20 + 3
(b) 70,00,000 + 2,00,000 + 4,000 + 50 + 8
(c) 5,00,00,000 + 6,00,000 + 40,000 + 3,000 + 800 + 5
Sol.
(a) 1,00,000 + 70,000 + 8,000 + 900 + 20 + 3 = 1,78,923
(b) 70,00,000 + 2,00,000 + 4,000 + 50 + 8 = 72,04,058
(c) 5,00,00,000 + 6,00,000 + 40,000 + 3,000 + 800 + 5 = 5,06,43,805
Problem 11.
Write the following numbers in words.
(a) 1,78,040
(b) 23,06,789
(c) 5,03,56,033
Sol.
(a) 1,78,040 = One lakh seventy-eigth thousand forty
(b) 23,06,789 = Twenty-three lakh six thousand seven hundred eighty-nine
(c) 5,03,56,033 = Five crore three lakh fifty-six thousand thirty-three
Problem 12.
Write the following numbers in figures.
(a) Six lakh twenty thousand eighty-seven
(b) Twenty-nine lakh forty thousand thirty-eight
(c) Three crore five lakh thirty-six thousand seven
Sol.
(a) Six lakh twenty thousand eighty-seven = 6,20,087
(b) Twenty-nine lakh forty thousand thirty-eight = 29,40,038
(c) Three crore five lakh thirty-six thousand seven = 3,05,36,007
Multiple Choice Questions
Problem 1.
If N is the set of all natural numbers and W is the set of all whole numbers then overlapped part of N represent of which one of the following number ?

(A) 1
(B) 0
(C) 2
(D) all of these
Problem 2.
From the following sets of numbers, which one of the following is the set of co primes ?
(A) {8, 16}
(B) {10, 100}
(C) {3, 5}
(D) All of these
Problem 3.
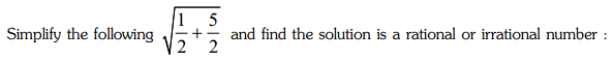
(A) irrational number
(B) Rational number
(C) Solution is zero
(D) All of these
Problem 4.
How many prime numbers are there between 100 and 125?
(A) 5
(B) 6
(C) 3
(D) All of these
Problem 5.
Two consecutive prime numbers are given, if one of them is 5 then the second number is:
(A) 3
(B) 7
(C) 9
(D) All of these
Problem 6.
If the sum of x + (y + z) = m + n then the sum of (y + z) + x is?
(A) m – n
(B) n – m
(C) m + n
(D) All of these
Problem 7.
The sum of difference of two whole numbers is a whole number then the product of two whole numbers is?
(A) Prime number
(B) Whole number
(C) Composite number
(D) All of these
Problem 8.
Simplify the (34 + 20) × 2 an find the multiplicative inverse of the resulting simplification:
(A) 2/108
(B) 1/108
(C) 3/108
(D) All of the above
Problem 9.
The division of y by x is z then the division of x by y is?
(A) z
(B) Other than z
(C) Less than z
(D) All of these
Problem 10.
How many different three digit numbers can be obtained by using the digits, 0, 1, 3 without repeating any digit in the number?
(A) 4
(B) 5
(C) 3
(D) 2
Problem 11.
Which one of the following is the smallest seven digit number having four different digits?
(A) 1230000
(B)0000123
(C) 1000023
(D) 1000032
Problem 12.
Find the value of 6 + 2[3 + 5{ 28 – 12(12 – 10)}]
(A) 56
(B) 52
(C) 53
(D) Both (A) and (C)
Problem 13.
A man gets pass for 1 year for Rs. 1500. If the man has been paid 11 payments then find the amount paid by him:
(A) Rs. 16500
(C) 17000
(C) Rs. 17500
(D) Both (A) and (C)
Problem 14.
The successor of the lowest composite number is?
(A) 6
(B) 5
(C) 3
(D) 4
Problem 15.
Smallest four digit number is divided by smallest prime number. Find the predecessor of the quotient:
(A) 500
(B) 501
(C) 499
(D) 599
Problem 16.
Which one of the following is not correct?
(A) Successor of a number can be obtained by adding 1
(B) The difference between successor and predecessor of a number is smallest composite number
(C) Successor of greatest 5 digit number is smallest six digit number and predecessor of smallest 6 digit number is greatest 5 digit number
(D) The difference between lowest natural number and whole number is 1
Problem 17.
M and N are co-prime numbers, M represents lowest odd prime number. Which one of the following is the factor of their product?
(A) 12
(B) 24
(C) 10
(D) 20
Problem 18.
8m – 145 = Greatest 5 digit number, find the value of m.
(A) 12618
(B)12718
(C) 12818
(D)12518
Problem 19.
Which on of the following is the set of the single digit prime number?
(A) {0,1,2,3,5,7}
(B) {2,3,5,7}
(C) {2,3,4,5,7}
(D) {0,1,2,51}
Problem 20.
Smallest 3 digit number is multiplied by smallest prime number and smallest composite number is added to it. Find the number
(A) 200
(B) 204
(C) 206
(D) 202
Problem 21.
A man takes rest for 10 minutes after every 30 minute, if he runs 2 km in 10 minutes, find the distance covered by him in 80 minutes:
(A) 11 km
(B) 7 km
(C) 10 km
(D) 12 km
Problem 22.
Two cars, one red coloured and another blue coloured are running in a racing competition. The track is 500 km long. Speed of red car in the beginning is 350 km/hour which reduces to 275 km/hour after running 45 minutes and speed of blue car in the beginning is 325 km/hour which increases to 350 km/hour after running 45 minutes. Which car would win the race?
(A) Red car
(B) Blue car
(C) Both will complete the race at equal time
(D) Data is insufficient to answer the question
Problem 23.
A fan rotates on its shaft around 5 times in one second. How many times does the fan rotate in a day if there was no electricity for 2 hours?
(A) 396000 times
(B) 39600 times
(C) 395000 times
(D) 398000 times
We hope the NCERT Solutions for Class 6 Maths Chapter 1 Knowing Our Numbers help you. If you have any query regarding NCERT Solutions for Class 6 Maths Chapter 1 Knowing Our Numbers, drop a comment below and we will get back to you at the earliest.